什么是感知机 | 最简单的人工神经网络
什么是感知机 | 最简单的人工神经网络
什么是感知机
感知机是 1957 年由 Frank Rosenblatt 提出的一种最简单的人工神经网络架构,主要用于二元分类。
感知机是一种执行二元分类的神经网络,它将输入特征映射到输出决策,通常将数据分类为两个类别之一,例如 0 或 1。
感知机由一个完全连接到输出节点的输入节点层组成。它特别擅长学习线性可分模式。它利用了一种称为阈值逻辑单元(TLU)的人工神经元变体,该变体由麦卡洛克和沃尔特·皮茨在 20 世纪 40 年代首次提出。这个基础模型在更高级的神经网络和机器学习算法的发展中发挥了关键作用。
感知机的类型
单层感知机是一种感知机,它仅限于学习线性可分模式。它适用于可以通过直线将数据划分为不同类别的任务。虽然其简单性使其功能强大,但在处理输入和输出之间关系非线性的更复杂问题时,它却难以应对。
多层感知机具有更强的处理能力,因为它由两个或更多层组成,擅长处理数据中更复杂的模式和关系。
感知器的基本组成部分
- 输入特征:感知器接收多个输入特征,每个特征代表输入数据的一个特性。
- 权重:每个输入特征被分配一个权重,该权重决定了其对输出的影响。这些权重在训练过程中进行调整,以找到最优值。
- 求和函数:感知器计算其输入的加权总和,将输入与其对应的权重结合起来。
- 激活函数:加权总和通过 Heaviside 阶跃函数进行处理,将其与阈值进行比较,以产生二进制输出(0 或 1)。
- 偏差:偏差项帮助感知器独立于输入进行调整,提高其学习灵活性。
- 学习算法:感知器使用学习算法(如感知器学习规则)调整其权重和偏差,以最小化预测误差。
感知器是如何工作的?
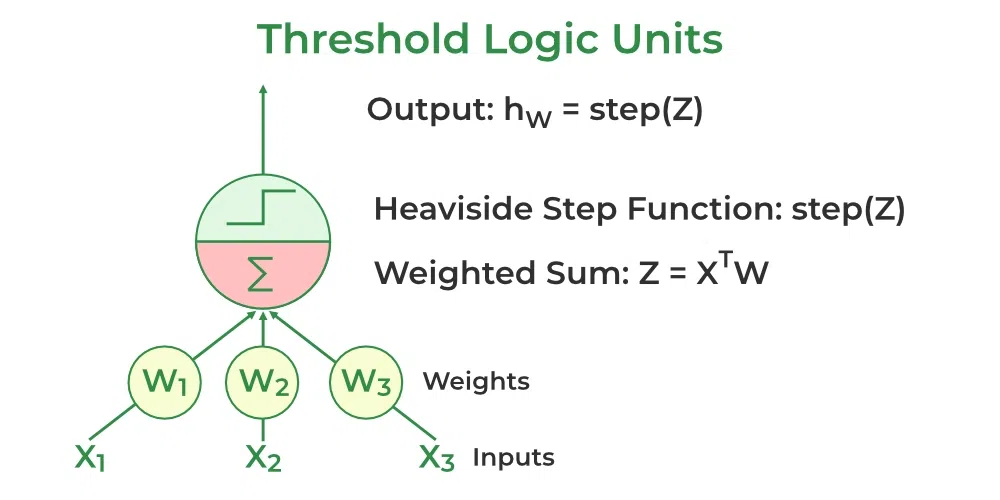
感知器的每个输入节点都被分配一个权重,表示该输入在确定输出中的重要性。感知器的输出是通过输入的加权求和计算得出的,然后通过激活函数来决定感知器是否被激活。
加权求和的计算方式如下:
$$ z = w_1x_1 + w_2x_2 + \cdots + w_nx_n = X^TW $$
阶跃函数将这个加权求和与一个阈值进行比较。如果输入大于阈值,输出为 1;否则输出为 0。这是感知器中最常用的激活函数,通常用 Heaviside 阶跃函数表示:
$$ h(z) = \left{ \begin{array}{ll} 0 & \text{if } z < \text{Threshold} \ 1 & \text{if } z \geq \text{Threshold} \end{array} \right. $$
感知器由一个阈值逻辑单元(TLU)层组成,每个 TLU 都与所有输入节点完全连接。
在一个全连接层(也称为密集层)中,一层中的所有神经元都与前一层的每个神经元连接。
全连接层的输出计算如下:
$$ f_{W,b}(X) = h(XW + b) $$
$X$是输入,$W$是每个输入神经元的权重,$b$是偏差,$h$是阶跃函数。
在训练过程中,感知器的权重会调整以最小化预测输出与实际输出之间的差异。这通过使用监督学习算法(如 delta 规则或感知器学习规则)来实现。
权重更新公式为:
$$ w_{i,j} = w_{i,j} + \eta \left( y_{j} - \hat{y}{j} \right) x{i} $$
概念不想写了,参照原文
Numpy实现全连接单层感知机
import numpy as np
np.random.rand(10) @ np.random.rand(10)
np.float64(1.7952493740730333)
# 构建感知器模型类 class Perceptron: def __init__(self, num_inputs, learning_rate=0.1): """ 初始化感知器 参数: num_inputs: 输入特征的数量 learning_rate: 学习率,控制每次权重更新的步长,默认为0.01 """ # 初始化权重向量,包含偏置项(weights[0])和特征权重(weights[1:]) # 使用随机数初始化,权重维度为特征数量+1(加上偏置项) self.weights = np.random.rand(num_inputs + 1) * 0.01 self.learning_rate = learning_rate def linear(self, inputs): """ 计算线性组合: z = w·x + b 参数: inputs: 输入特征向量 返回: 线性组合的结果 """ # 计算特征权重与输入的点积,并加上偏置项 Z = inputs @ self.weights[1:] + self.weights[0] return Z def Heaviside_step_fn(self, z): """ Heaviside阶跃函数(激活函数) 参数: z: 线性组合的结果 返回: 如果z>=0,返回1;否则返回0 """ if z>=0: return 1 else: return 0 def predict(self, inputs): """ 预测函数:对输入数据进行预测 参数: inputs: 输入特征向量或特征矩阵 返回: 预测结果(0或1) """ # 首先计算线性组合 Z = self.linear(inputs) try: # 如果输入是批量数据,逐个应用阶跃函数 pred = [] for z in Z: pred.append(self.Heaviside_step_fn(z)) except: # 如果输入是单个样本,直接应用阶跃函数 return self.Heaviside_step_fn(Z) return pred def loss(self, prediction, target): """ 计算损失:预测值与目标值的差异 参数: prediction: 模型预测值 target: 真实标签 返回: 预测误差 """ loss = target - prediction return loss def train(self, inputs, target): """ 训练函数:更新权重 参数: inputs: 输入特征 target: 目标值 """ # 获取预测值 prediction = self.predict(inputs) # 计算误差 error = self.loss(prediction, target) print(error) # 更新权重 self.weights[1:] += self.learning_rate * np.dot(error,inputs) # 更新偏置 self.weights[0] += self.learning_rate * error * 1 def fit(self, X, y, num_epochs): """ 模型训练主函数 参数: X: 训练数据特征矩阵 y: 训练数据标签 num_epochs: 训练轮数 """ # 进行多轮训练 for epoch in range(num_epochs): # 对每个训练样本进行训练 for inputs, target in zip(X, y): self.train(inputs, target)
from sklearn.datasets import make_blobs # 用于生成人工数据集 import matplotlib.pyplot as plt # 用于数据可视化 from sklearn.model_selection import train_test_split # 用于数据集划分 from sklearn.preprocessing import StandardScaler # 用于特征标准化
X, y = make_blobs(n_samples=1000, n_features=10, centers=2, cluster_std=3, random_state=23)
model = Perceptron(10)
# 将数据集划分为训练集和测试集 # test_size=0.2 表示测试集占20% # random_state: 随机种子,确保划分结果可复现 # shuffle=True: 在划分前对数据进行随机打乱 X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=23, shuffle=True )
X_pre = model.predict(X_test) correct = sum(1 for p, t in zip(X_pre, y_test) if p == t) total = len(X_pre) result = correct / total * 100 print(f"初始正确率为{result}%")
初始正确率为41.5%
print(f"当前感知机参数:\n{model.weights}")
当前感知机参数: [0.0022028 0.00500288 0.00061814 0.00377461 0.0039365 0.00233322 0.00179385 0.00342842 0.00954213 0.00502752 0.00568346]
model.fit(X_train,y_train,1)
1 -1 0 -1
print(f"训练后感知机参数:\n{model.weights}")
训练后感知机参数: [-0.0977972 -1.10058644 -0.79820497 -0.3409109 0.84470909 1.22607636 0.65520488 2.34404683 -0.6905295 -1.46827118 -0.57119956]
X_pre = model.predict(X_test)
correct = sum(1 for p, t in zip(X_pre, y_test) if p == t) total = len(X_pre) result = correct / total * 100 print(f"正确率为{result}%")
正确率为100.0%
import matplotlib.pyplot as plt from sklearn.decomposition import PCA pca = PCA(n_components=2) X_pca = pca.fit_transform(X_test) plt.scatter(X_pca[:, 0], X_pca[:, 1], c=X_pre, alpha=0.6, cmap='viridis', edgecolor='k') plt.xlabel('PCA Component 1') plt.ylabel('PCA Component 2') plt.show()

Pytorch 实现全连接单层感知机
import torch import torch.nn as nn
class TorchPerceptron(nn.Module): def __init__(self, num_inputs): super(TorchPerceptron, self).__init__() self.linear = nn.Linear(num_inputs, 1) def heaviside_step_fn(self,Z): Class = [] for z in Z: if z >=0: Class.append(1) else: Class.append(0) return torch.tensor(Class) def forward(self, x): Z = self.linear(x) return self.heaviside_step_fn(Z)
torch_model = TorchPerceptron(10)
X_train = torch.from_numpy(X_train).to(torch.float32) X_test = torch.from_numpy(X_test).to(torch.float32) y_train = torch.from_numpy(y_train).to(torch.float32) y_test = torch.from_numpy(y_test).to(torch.float32)
y_pre = torch_model.forward(X_test)
print(f"当前准确率:{sum(1 for yt,yp in zip(y_test,y_pre) if yt == yp)/len(y_test)* 100}%")
当前准确率:41.0%
for batch in range(10): for x,y in zip(X_train, y_train): y_p = torch_model.forward(x) loss = y - y_p learning_rate = 0.001 w = torch_model.linear.weight b = torch_model.linear.bias c = torch.matmul(loss.reshape(1,-1),x.reshape(1,-1)) with torch.no_grad(): w += learning_rate * c b += learning_rate * loss * 1 print(w) print(b)
Parameter containing: tensor([[-0.1725, -0.1792, 0.0105, -0.0515, 0.2428, 0.0905, 0.1281, -0.0349, 0.0364, -0.1594]], requires_grad=True) Parameter containing: tensor([0.0215], requires_grad=True) Parameter containing: tensor([[-0.1743, -0.1801, 0.0066, -0.0418, 0.2391, 0.0953, 0.1424, -0.0367, 0.0178, -0.1424]], requires_grad=True) Parameter containing: tensor([0.0205], requires_grad=True) Parameter containing: tensor([[-0.1790, -0.1745, 0.0089, -0.0360, 0.2322, 0.1056, 0.1535, -0.0428, 0.0005, -0.1312]], requires_grad=True) Parameter containing: tensor([0.0205], requires_grad=True) Parameter containing: tensor([[-0.1776, -0.1818, 0.0035, -0.0305, 0.2246, 0.1078, 0.1604, -0.0489, -0.0076, -0.1230]], requires_grad=True) Parameter containing: tensor([0.0195], requires_grad=True) Parameter containing: tensor([[-0.1765, -0.1849, -0.0043, -0.0289, 0.2231, 0.1023, 0.1633, -0.0511, -0.0108, -0.1207]], requires_grad=True) Parameter containing: tensor([0.0185], requires_grad=True) Parameter containing: tensor([[-0.1802, -0.1812, -0.0016, -0.0280, 0.2124, 0.1078, 0.1719, -0.0610, -0.0169, -0.1187]], requires_grad=True) Parameter containing: tensor([0.0185], requires_grad=True) Parameter containing: tensor([[-0.1792, -0.1843, -0.0094, -0.0264, 0.2108, 0.1024, 0.1747, -0.0631, -0.0201, -0.1165]], requires_grad=True) Parameter containing: tensor([0.0175], requires_grad=True) Parameter containing: tensor([[-0.1782, -0.1874, -0.0172, -0.0248, 0.2093, 0.0969, 0.1776, -0.0652, -0.0233, -0.1142]], requires_grad=True) Parameter containing: tensor([0.0165], requires_grad=True) Parameter containing: tensor([[-0.1782, -0.1874, -0.0172, -0.0248, 0.2093, 0.0969, 0.1776, -0.0652, -0.0233, -0.1142]], requires_grad=True) Parameter containing: tensor([0.0165], requires_grad=True) Parameter containing: tensor([[-0.1782, -0.1874, -0.0172, -0.0248, 0.2093, 0.0969, 0.1776, -0.0652, -0.0233, -0.1142]], requires_grad=True) Parameter containing: tensor([0.0165], requires_grad=True)
y_pre = torch_model.forward(X_test)
print(f"当前准确率:{sum(1 for yt,yp in zip(y_test,y_pre) if yt == yp)/len(y_test)* 100}%")
当前准确率:100.0%
总结
感知机的局限性
- 仅限于线性可分问题
- 处理不可分数据时难以收敛
- 训练需要标记数据
- 对输入缩放敏感
- 缺乏隐藏层进行复杂决策
实战
使用多层感知机实现对鸢尾花数据集分类
from sklearn.datasets import load_iris
iris = load_iris(return_X_y=True, as_frame=True)
iris_x = iris[0][:100] iris_y = iris[1][:100]
X_train,X_test,y_train,y_test = train_test_split( iris_x, iris_y, test_size=0.2, random_state=10, )
X_train = torch.from_numpy(X_train.values).to(torch.float32) X_test = torch.from_numpy(X_test.values).to(torch.float32) y_train = torch.from_numpy(y_train.values).to(torch.float32) y_test = torch.from_numpy(y_test.values).to(torch.float32)
iris_model = TorchPerceptron(4)
iris_pre = iris_model(X_test)
print(f"当前准确率:{sum(1 for yt,yp in zip(y_test,iris_pre) if yt == yp)/len(y_test)* 100}%")
当前准确率:55.00000000000001%
for batch in range(100): for x,y in zip(X_train,y_train): y_pre = iris_model(x) loss = y - y_pre learning_rate = 0.001 w = iris_model.linear.weight b = iris_model.linear.bias c = torch.matmul(loss.reshape(1,-1),x.reshape(1,-1)) with torch.no_grad(): w += learning_rate * c b += learning_rate * loss * 1
iris_pre = iris_model(X_test)
iris_pre
tensor([0, 0, 0, 0, 1, 0, 1, 1, 0, 1, 0, 0, 1, 1, 1, 1, 1, 0, 1, 0])
print(f"当前准确率:{sum(1 for yt,yp in zip(y_test,iris_pre) if yt == yp)/len(y_test)* 100}%")
当前准确率:95.0%
多层感知机
class NumpyMultiLayerPerceptron(): def __init__(self, input_size: int, hindder_layer: list[int], output_size: int, learn_rate = 0.001): self.input_size = input_size self.hindder_layer= hindder_layer self.output_size = output_size self.learn_rate = learn_rate layer_size = [input_size] + hindder_layer + [output_size] self.w = [] self.b = [] for i in range(len(layer_size) - 1): self.w.append(np.random.rand(layer_size[i], layer_size[i+1]) * 0.1) self.b.append(np.random.rand(1, layer_size[i+1]) * 0.1) def relu(self, X): return np.maximum(0,X) def relu_derivative(self, x): """ReLU的导数""" return (x > 0).astype(float) def softmax(self, x): exp_x = np.exp(x - np.max(x, axis=1, keepdims=True)) return exp_x / np.sum(exp_x, axis=1, keepdims=True) def forward(self, X): self.activations = [X] # 存储每一层的激活值 self.z_values = [] # 存储每一层的加权和(激活前) for i in range(len(self.w) - 1): z = X @ self.w[i] + self.b[i] self.z_values.append(z) X = self.relu(z) self.activations.append(X) z = self.activations[-1] @ self.w[-1] + self.b[-1] self.z_values.append(z) X = self.softmax(z) self.activations.append(X) return X def backward(self, X, y): # 前向传播 output = self.forward(X) batch_size = X.shape[0] # 将标签转换为one-hot编码 y_onehot = np.eye(self.output_size)[y] # 计算输出层误差(使用交叉熵损失) error = output - y_onehot # 存储梯度 gradients = [] # 输出层梯度 dW = self.activations[-2].T @ error / batch_size db = np.sum(error, axis=0, keepdims=True) / batch_size gradients.append((dW, db)) # 隐藏层梯度反向传播 for i in range(len(self.w)-2, -1, -1): error = error @ self.w[i+1].T * self.relu_derivative(self.z_values[i]) dW = self.activations[i].T @ error / batch_size db = np.sum(error, axis=0, keepdims=True) / batch_size gradients.append((dW, db)) # 反转梯度列表,使其与权重顺序一致 gradients = gradients[::-1] # 更新权重和偏置 for i in range(len(self.w)): self.w[i] -= self.learn_rate * gradients[i][0] self.b[i] -= self.learn_rate * gradients[i][1] def predict(self, X): return np.argmax(self.forward(X))
iris_x = iris[0].values iris_y = iris[1].values
X_train,X_test,y_train,y_test = train_test_split( iris_x, iris_y, test_size=0.2, random_state=10, )
model = NumpyMultiLayerPerceptron(4, [64, 32, 16], 3)
f"当前准确率{sum(1 for i,d in enumerate(X_test) if model.predict(d) == y_test[i])/len(X_test)*100}%"
'当前准确率43.333333333333336%'
for batch in range(1000): for x,y in zip(X_train,y_train): model.backward(x.reshape(1,-1),y)
f"当前准确率{sum(1 for i,d in enumerate(X_test) if model.predict(d) == y_test[i])/len(X_test)*100}%"
'当前准确率96.66666666666667%'
Pytorch
class TorchMultiLayerPerceptron(nn.Module): def __init__(self, input_size, hindden_layer, output_size, learn_rate = 0.01): super().__init__() layers = [nn.Linear(input_size,hindden_layer[0])] layers.append(nn.ReLU()) for i in range(len(hindden_layer) - 1): layers.append(nn.Linear(hindden_layer[i], hindden_layer[i+1])) layers.append(nn.ReLU()) layers.append(nn.Linear(hindden_layer[-1], output_size)) # layers.append(nn.Softmax(dim=1)) self.model = nn.Sequential(*layers) self.input_size = input_size self.hindden_layer = hindden_layer self.output_size = output_size self.learn_rate = learn_rate def forward(self, x): return self.model(x) def backward(self, X, y): # 清空梯度 self.model.zero_grad() # 前向传播 output = self.forward(X) y = y.long().reshape(-1) # 计算交叉熵损失 criterion = nn.CrossEntropyLoss() loss = criterion(output, y) # 自动反向传播(PyTorch 自动计算梯度) loss.backward() # 手动更新参数(模拟 NumPy 的梯度下降) with torch.no_grad(): # 禁用 Autograd,避免跟踪更新操作 for param in self.model.parameters(): param -= self.learn_rate * param.grad def predict(self, X): return torch.argmax(self.forward(X), dim=1)
iris_x = iris[0].values iris_y = iris[1].values
X_train,X_test,y_train,y_test = train_test_split( iris_x, iris_y, test_size=0.2, random_state=10, )
X_train = torch.from_numpy(X_train).to(torch.float32) X_test = torch.from_numpy(X_test).to(torch.float32) y_train = torch.from_numpy(y_train).to(torch.long) y_test = torch.from_numpy(y_test).to(torch.long)
model = TorchMultiLayerPerceptron(4, [64, 32, 16], 3) model
TorchMultiLayerPerceptron( (model): Sequential( (0): Linear(in_features=4, out_features=64, bias=True) (1): ReLU() (2): Linear(in_features=64, out_features=32, bias=True) (3): ReLU() (4): Linear(in_features=32, out_features=16, bias=True) (5): ReLU() (6): Linear(in_features=16, out_features=3, bias=True) ) )
f"当前准确率{sum(1 for i,d in enumerate(X_test) if model.predict(d.reshape(1,-1)) == y_test[i])/len(X_test)*100}%"
'当前准确率43.333333333333336%'
for batch in range(1000): for x,y in zip(X_train,y_train): model.backward(x.reshape(1,-1),y)
f"当前准确率{sum(1 for i,d in enumerate(X_test) if model.predict(d.reshape(1,-1)) == y_test[i])/len(X_test)*100}%"
'当前准确率96.66666666666667%'